2025湖南中考数学真题变化及解读

       2025年湖南省初中学业水平考试试题坚持落实《义务教育数学课程标准（2011年版）》的总体要求，渗透《义务教育数学课程标准（2022年版）》的部分内容及精神理念.与2024年湖南中考数学试题相比，2025年湖南中考数学试题在题型结构、知识点覆盖上相对稳定，注重基础知识的考查，难易度区分有效，试卷整体新增及强化的趋势主要有以下几方面：

趋势1：创设真实任务情境，彰显数学的应用价值及育人功能

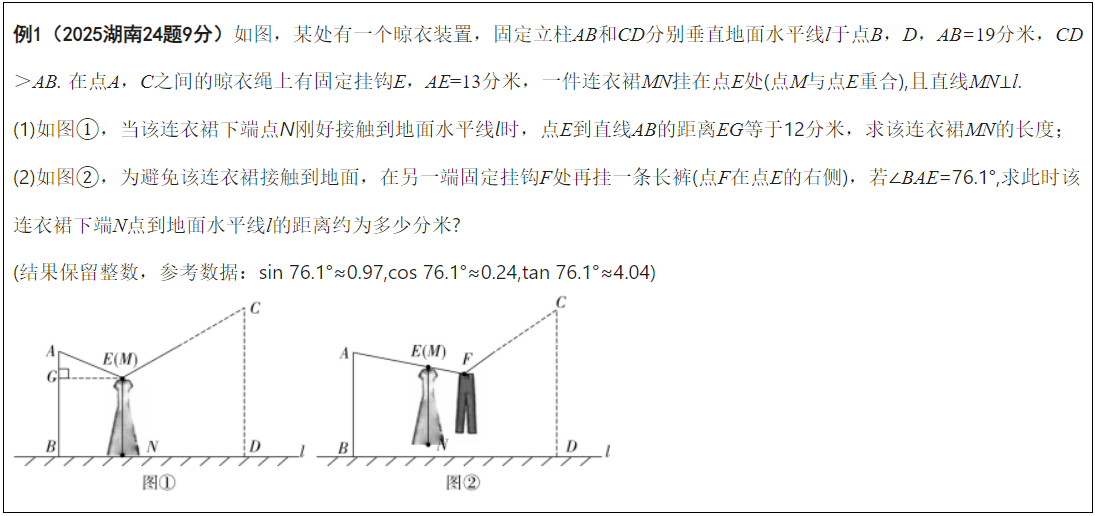
       【趋势解读】例1以“晾衣装置”为背景，考查锐角三角函数的测量，培养学生提取、处理、分析和利用信息的能力，引导学生用数学眼光、思维和语言去观察、思考和表达现实世界，试题设问贴合现实,体现数学的应用价值和育人功能，还使得考试内容与学生的生活经验、社会体验相结合，真实地考查学生理解和运用所学知识与技能解决问题的能力，引导学生感受社会的发展、关注生活的美好.

       【备考建议】教师在复习备考过程中，要关注教材中实际背景习题与例题，但要明确教材的局限性，其与飞速发展的现代生活有一定距离，且教材是针对全国学生和老师，而中考是省级水平的考试，更多关注地域文化和特色，因此在日常教学中，可类比教材，用发现的视角去挖掘本土文化特征，让本土相关的优秀文化和真实情境走进试题.同时在设置试题时，要注意情境和问题的真实性、合理性，体现数学在实际生活中的应用价值.也可以通过练习2025全国其他地市中考典型的真实情境试题，提高学生用数学知识解决现实问题的能力，具体如下：

趋势2：关注跨学科试题，培养学生解决综合问题的能力

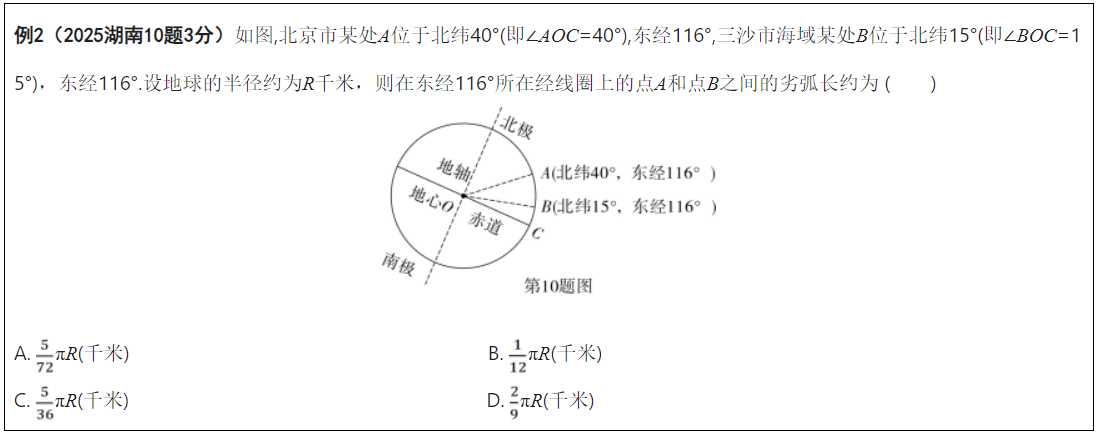       【趋势解读】例2以地理知识经纬度为背景，利用数学学科知识，考查弧长的计算.试题融入了地理学科的背景，但未在跨学科知识上为难学生，利用数学学科知识即可解决.教育部 2019年11月发布的《关于加强初中学业水平考试命题工作的意见》指出“结合不同学科特点，合理设置试题结构，减少机械记忆试题和客观性试题比例，提高探究性、开放性、综合性试题比例，积极探索跨学科命题”.2022年版课标中提到“初中阶段综合与实践领域，可采取项目式学习的方式，以问题解决为导向，整合数学与其他学科的知识和思想方法，让学生从数学的角度观察与分析、思考与表达、解决与闸释社会生活以及科学技术中遇到的现实问题.例2落实了跨学科.

       【备考建议】在实际教学过程中,要实现跨学科整合,需了解学生的知识积累和学习规律,从学生感兴趣的点出发,首先教师在平时讲课过程中可以适当地引入与所讲内容相关的其他学科的背景,如在讲不等式的知识时,引入凸透镜成像规律:讲函数知识时,引入速度公式,密度公式、重力公式等;其次可以带领学生完成 2022年版课标内容中给出的实例,通过数学与科学、物理、化学、地理等学科知识的结合,提升学生解决跨学科类试题的能力,最后也可以通过练习2025全国其他地市中考典型的跨学科试题，提升学生综合解决问题的能力，具体如下：

趋势3：重视试题开放性，助力高层次思维创造

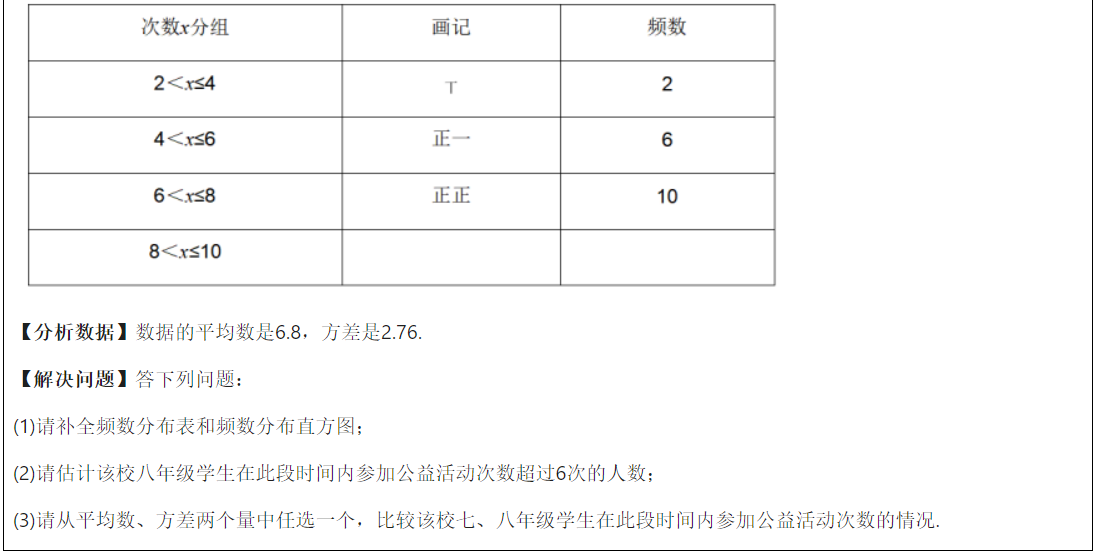       【趋势解读】《初中学业水平考试关键问题命题指南》中强调“相较封闭性试题，开放性试题更能给考生提供在问题解决中主动创造的机会，更强调考生的建构性反应，更能够为考查高层次思维创造条件…….开放性试题更有利于对核心素养的考查，更加符合新课程的评价理念，因此，在考试中应适度增加试题的开放性或适当提高开放性试题的比例.”例3通过条件开放的形式考查统计的应用，同时通过对公益活动次数的统计分析，考查学生数据整理、分析及用样本估计总体的能力，强调统计观念培养.

       【备考建议】开放性试题主要分为结论开放、解题策略开放(选择解题策略、自主寻求解题策略)，条件开放(添加/补充条件、选择条件、组合多选)、命题特点就是要求学生解题的思路要开放，思维要开阔，因此教师在平时的教学中，要注重创设合理的问题情境，引导学生积极探索，让学生思维活跃起来，提高学生综合剖析问题、解决问题的能力，使学生养成创新意识与独立思考的习惯.

趋势4：重视代数推理，提升学生数学的思维推理能力

       【趋势解读】例4题为二次函数综合题，解题需构建函数模型，结合几何图形性质（如直线平行、角度关系 ），将代数与几何知识融合，对学生思维要求高，能有效区分不同层次学生水平，重点考查了学生的模型观念、推理能力、几何直观、抽象能力等核心素养及综合运用知识的能力.

       【备考建议】2022年版课标在数与代数领域增加了推理要求，突出代数推理，明确提出“了解代数推理”的要求，为高中代数的学习奠定基础，是“初高衔接”的重要举措.在教学中，要重视算理、算法和规律的过程探究，对代数式进行多种变形，发现其特征.教师也要带领学生深入理解二次函数的定义、性质、图像特征，如开口方向、顶点坐标、对称轴、与坐标轴的交点等.掌握二次函数的解析式求法，包括一般式、顶点式、交点式，以及它们之间的转换.熟练掌握二次函数与一元二次方程、不等式之间的关系，能通过函数图像和代数方法解决相关问题.在解题过程中，要注重逻辑推理的严密性，每一步都要有充分的依据.学会从已知条件出发，逐步推导出结论，避免出现跳跃式思维或错误的推理.

 Ps 

1.下载本文、查看更多中考真题变化及解读、下载新变化趋势题，请点击本页上方返回首页→登录武老师·中考云备考

2.如您还没有账号，请点击本页上方免费试用→扫码添加云备考顾问申请开通